Говоря о нашей Вселенной, мы различаем «Вселенную» и «наблюдаемую Вселенную». Последнее включает лишь то, что мы можем видеть. Я не имею в виду, что у нас есть технология, чтобы реально «видеть» всю наблюдаемую вселенную. Я имею в виду под «наблюдаемыми» все объекты, свет от которых в принципе мог дойти до нас, учитывая время жизни Вселенной, скорость света и историю и будущее расширения Вселенной. Возраст Вселенной составляет 13,8 миллиардов лет. Из-за конечности скорости света мы не можем видеть то, что расположено от нас настолько далеко, что свету на путешествие до нас потребовалось бы больше времени, чем существует Вселенная. Это не технологическое ограничение – это ограничение того, существует ли в принципе тот свет, который мы могли бы увидеть, будь у нас в распоряжении любая технология.

Когда мы смотрим на окраины наблюдаемой Вселенной, мы смотрим в прошлое. Если свету потребовалось 13,7 миллиарда лет, чтобы дойти до нас, значит, мы видим Вселенную такой, какой она была 13,7 миллиарда лет назад, а не такой, какая она сейчас.
В целом Вселенная, возможно, бесконечна. Заявить это просто, но эту концепцию очень сложно представить, если подумать. Одним из решений этой проблемы можно назвать предложение не заморачиваться этим. Если вы задаёте себе вопросы типа «как она может расширяться, если она бесконечна», вы неправильно представляете себе бесконечность. Бесконечность – это концепция, а не число.
Однако Вселенной не обязательно быть бесконечной. Согласно ОТО, существуют и другие возможности. Я разделю их на две категории, но поговорим мы подробно только об одной из них.
Интересные топологии
Возможно, что у Вселенной интересная топология. Топология отличается от геометрии. Геометрия включает такие вещи, как длину линий, радиус кривизны, суммы углов полигонов и т.п. Топология занимается тем, как соединены между собой разные части пространства.
Рассмотрим, в качестве примера, классическую игру Asteroids:
Игра идёт в очень маленькой двумерной вселенной. Геометрия вселеннойAsteroids евклидова – параллельные линии не пересекаются, отношение длины окружности к диаметру равно π, сумма трёх внутренних углов треугольника равна 180° и так далее. Но если вы играли в эту игру, вы знаете, что если уйти за левый край экрана, то вернёшься с правого края. Если уйти с верхнего края, то вернёшься с нижнего. Вселенная не имеет границ, вы никогда не упрётесь в границу, или край. Но она конечна. Её топология тороидальная – такая же, как у поверхности бублика, хотя геометрия её отличается от геометрии бублика (поверхность бублика искривлена).
Возможно, что наша Вселенная ведёт себя так же. У неё может быть плоская геометрия, но такая топология, что если вы двигаетесь в одном направлении, вы вернётесь туда, откуда пришли. Если у неё действительно такая топология, то она проявляется на масштабах крупнее наблюдаемой Вселенной. Иначе мы бы увидели подтверждение такой топологии (например, части космоса повторяли бы друг друга, если долго идти в одном направлении) в микроволновом космическом излучении.
Так что пока мы примем, что у Вселенной нет никаких интересных топологий. Либо это бесконечное пространство, либо это конечное пространство, представляющее собой трёхмерный эквивалент поверхности сферы.
Возможные геометрии Вселенной
Геометрия Вселенной не обязана быть евклидовой. В зависимости от общей плотности энергии (включая плотность обычной материи, тёмной материи и тёмной энергии), для кривизны Вселенной существуют три возможности.
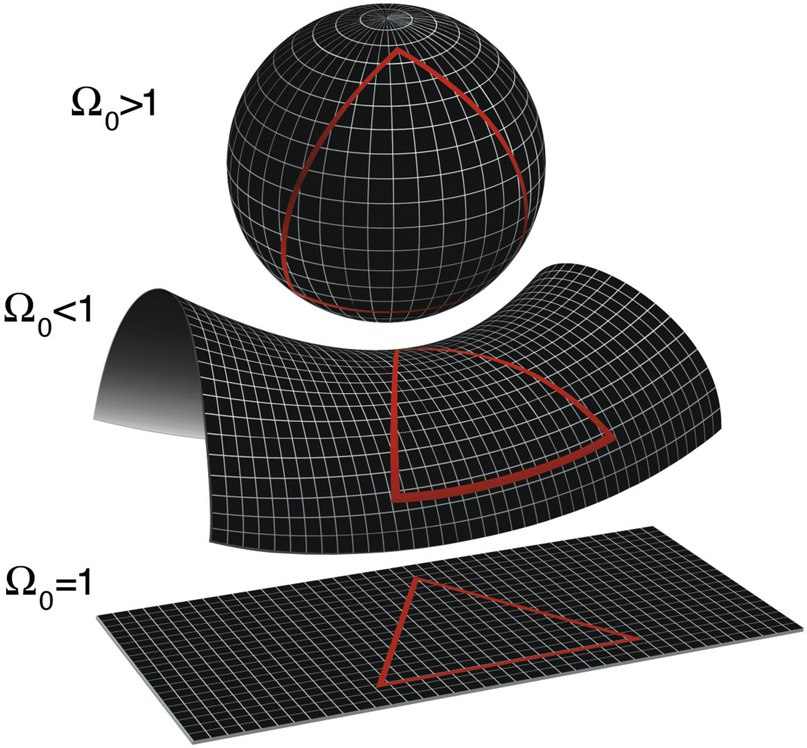
Параметр Ω – удобный способ обсуждения плотности Вселенной. Существует критическая плотность, зависящая от текущей скорости расширения Вселенной. Она составляет 9*10^(-30) гр/см. Вроде бы немного, но учтите, что Вселенная практически пустая. Земля – сравнительно плотное место по сравнению с большей частью Вселенной. Параметр Ω определяется, как отношение плотности Вселенной к критической. Если Ω = 1, то геометрия Вселенной плоская. Плоская – не значит двумерная, в том смысле, в котором вы привыкли говорить о плоскости. Это значит, что геометрия пространства евклидова, как та, что вы изучали в школе.
Если Ω>1, геометрия Вселенной закрытая. В этом случае геометрия у Вселенной будет такой же, как у трёхмерной поверхности четырёхмерной гиперсферы. Если это звучит непонятно, представьте себе это как трёхмерный эквивалент поверхности сферы. При этом у четырёхмерной гиперсферы не обязательно должно быть четвёртое пространственное измерение. Это просто означает, что геометрия Вселенной – как ведут себя параллельные линии, чему равна сумма углов треугольника, или отношение длины окружности к диаметру – такие же, как геометрия на поверхности сферы. Можно описать математику этой геометрии, используя только лишь три пространственных измерения, поэтому высшие измерения могут не понадобиться. Однако, для нужд нашего описания, стоит представить себе поверхность сферы, поскольку это поможет получить представление об устройстве такой вселенной. Поверхность сферы – двумерная закрытая вселенная. Помните, что вселенная – это поверхность. У неё нет центра, его нет в пределах вселенной – поскольку всё, что в ней содержится, находится на поверхности сферы и ни одна из её точек не отличается от других.
Если Ω<1, геометрия Вселенной открытая. Это представить уже труднее. Кусочек открытой трёхмерной вселенной не получится впихнуть для визуализации в три измерения, так, как это прокатывает с закрытой вселенной. Однако ближайшим двумерным эквивалентом будет седло или чипсы (являющиеся гиперболоидами, или гиперболическими параболоидами). Это безграничная и бесконечная вселенная. Она продолжается бесконечно. При этом она не плоская и у неё будет интересная геометрия. Геометрия нашей Вселенной Геометрию своей вселенной можно узнать несколькими способами. Например, можно построить в космосе треугольник из трёх прямых. Затем нужно измерить угол между каждыми из пар линий. Если вы сложите их и получите 180°, вы находитесь в плоской вселенной. Если сумма превысит 180°, это будет закрытая вселенная; если она будет меньше 180°, то это будет открытая вселенная. Проблема лишь в точности измерений. Либо нужно мерить эти углы с невероятной точностью, либо рисовать очень большие треугольники – такие, чтобы длина одной из его сторон приближалась к радиусу кривизны вашей вселенной. (Степень приближения зависит от точности измерения углов). По сути, мы это сделали. Измерения микроволнового космического излучения (МКИ) дали нам треугольники. Одна сторона треугольника получается из характерного размера флюктуаций в МКИ. Мы знаем их физический размер. Другие получаются из пути света, путешествующего с двух сторон этой флюктуации. Измеряя угол между лучами света, идущими с каждой из сторон, мы можем выяснить геометрию треугольника. Мы это сделали. Ответ: наша Вселенная плоская. Однако, как с любыми физическими величинами, в наших измерениях есть погрешность. Судя по последним подсчётам, значение Ω находится между 0,9916 и 1,0133, с 95% точностью. Это значит, что всё ещё существует возможность того, что наша Вселенная бесконечна (Ω≤1) или конечна (Ω>1).
Минимальный размер нашей Вселенной
Космос велик. Он просто огромен. Вы даже не поверите, насколько он умопомрачительно громаден. Вам может казаться, что от вашего дома до аптеки далеко, но это просто ерунда в сравнении с космосом.
Принесём извинения Дугласу Адамсу и подсчитаем размер нашей Вселенной.
Во-первых, возраст Вселенной составляет 13,8 миллиардов лет. Это очень долго по сравнению с нашими жизнями, но для Вселенной — возраст вполне подходящий. Край наблюдаемой Вселенной находится от нас на расстоянии 48 миллиардов световых лет. «Погодите-ка!»,- можете закричать вы. «Как свет может за 13,8 миллиардов лет преодолеть расстояние в 48 миллиардов световых лет!». Вспомните, что за то время, пока свет шёл к нам, Вселенная расширялась. В каком-то смысле свет пытался «нагнать» расширение. Это несовершенное описание и если вам знакома СТО, вы будете возражать. Но это имеет некий смысл в контексте ОТО.
Как этот размер соотносится с общим размером Вселенной? Если мы предположим, что Ω=1,0133, а это максимальная плотность энергии, соответствующая текущим данным, и, значит, наименьшая из закрытых вселенных – то сможем подсчитать размер Вселенной.
Поверхность сферы обозначает размер всей Вселенной, где Ω=1,0133. Матовая часть находится вне наблюдаемой нами Вселенной; кусочек сверху – наблюдаемая Вселенная. Радиус кривизны этой вселенной составляет 120 миллиардов световых лет. Её окружность – 760 миллиардов световых лет. Это значит, что диаметр наблюдаемой Вселенной составляет 1/8 от полной длины линии, которую нужно было бы провести в пространстве, чтобы она замкнулась на себя. Объём всей Вселенной в 100 раз превышает объём наблюдаемой. (Если вы возразите, что 83 не равно 100, вспомните, что пространство у нас неэвклидово и ваша интуиция по поводу радиусов и объёмов не работает).
Вспомним, что это минимальный размер Вселенной, согласно нашим данным. Большинство подозревает, что Вселенная реально неизмеримо больше, чем эта и может быть бесконечной.
Размер и судьба не связаны
Открыв любую книжку о космологии, написанную раньше 2000 года (и некоторые чуть более новые), вы, скорее всего, прочтёте, что закрытая Вселенная реколлапсирует, а открытая – вечно расширяется. Но это так, только если плотность тёмной энергии вселенной нулевая! Эти описания неявно подразумевали, что в нашей Вселенной доминирует материя и в этом случае геометрия и судьба Вселенной были сильно связаны. В такой вселенной, как наша, где существует тёмная энергия, судьба и геометрия не связаны так сильно. Тёмная материя и тёмная энергия влияют как на форму Вселенной, так и на её судьбу, но влияют по-разному. Что именно случится с нашей Вселенной, зависит от того, какой именно окажется тёмная энергия. Но если она такая, как её представляет себе большинство из нас, Вселенная будет расширяться вечно и галактические кластеры будут всё дальше разлетаться друг от друга. При этом неважно, плоская наша Вселенная, открытая или закрытая.
![]()


