Известно, что многие люди испытывают разную степень комфорта или дискомфорта в помещениях с разными пропорциями и разными сводами, а также вблизи от старинных и современных архитектурных сооружений, чувствуют себя по-разному у острых углов. В странах с древней историей традиционно применяются определённые архитектурные формы (в массах и в деталях), успешно зарекомендовавшие себя в данной местности. Над пирамидами и островерхими кровлями отдельные исследователи фиксировали своеобразные факелы незримого излучения. Что всё это значит?
Специалисты в области биоэнергоинформатики, биолокации, радиофизики и микроэнергетики, наверное, скажут, что речь может идти о незримых микроэнергетических потоках, возникающих под влиянием природных излучений в различных объектах среды обитания людей и животных. Можно ли выявить наличие этих микроэнергетических потоков без применения специальной и уникальной аппаратуры, чтобы использовать эту информацию в архитектурной и инженерной практике?
К сожалению, традиционные специалисты-ортодоксы (физики, биологи, экологи, архитекторы и др.) как правило, не могут ничего предложить для выяснения этого вопроса. Нам следует помнить, что сказал о таких специалистах германский философ Артур ШОПЕНГАУЭР (18-19. вв.): «Каждый принимает край своего кругозора за край света».
Согласно второму закону Ньютона можно сделать вывод, что в данной точке гравитационного пространства и при постоянном количестве данного вещества в данном материальном теле его вес, а также суммарный вес его элементов (деталей), являются постоянной величиной.
Однако было замечено, что этот вывод ошибочен!
Интересная информация по этому поводу имеется в книге У.Найманна «Электротехнические технологии» (Берлин, 198б). Поэтому, занимаясь в течение ряда лет вопросами микроэнергетики геометрических, архитектурных и декоративных форм о помощью биолокационных методов диагностики, мы решили провести пионерское исследование па¬радокса массы и веса с помощью аналитических весов рычажного типа. Обьектами исследования являлись:
- а) металлические тонкостенные геометрические тела полуоткрытого типа (без одной грани), непереналаживаемые;
- б) пластмассовые тонкостенные композиции, состоящие из одного или нескольких соосных конусов, переналаживаемые;
- в) пластмассовые тонкостенные композиции, состоящие из одной или нескольких соосных полусфер, переналаживаемые.
В качестве измерительного прибора применялись аналитические весы типа АДВ-200М, 2 кл., п/н 200 г, 1961 г. с точностью измерений до 4-го знака после запятой. Весы находились в постоянном месте, на массивном лабораторном столе-прилавке, в затенённом углу. Все измерения проводила зав. лабораторией химических исследований института Л. М.Дудкина — в отдельные дни, в интервале времени от 12 до 16 часов, при хорошей погоде.
Способы крепления объектов на весах: для металлических — подвешивание на крючке под коромыслом; для пластмассовых — установка на специальной стойке, входящей в композицию, на чашке весов.
В серии опытов с металлическими объёмными композициями вначале были изготовлены и взвешены плоские полуфабрикаты будущих тел (с медными проволочными петельками для подвешивания) — из листовой красной меди толщиной 1,0 мм с трёхслойным покрытием с внутренней стороны (синтетический клей, бумага, нитролак). Затем было выполнено формообразование объектов, исключительно путём сгибания полуфабрикатов, без резания и паяния. Наконец, все полученные композиции были взвешены, каждая в нескольких разных положениях относительно горизонтальной плоскости, в том числе отсутствующей гранью вниз и вверх.
Исследованиям подверглись следующие геометрические формы:
MI — тетраэдр (равнорёберный 4-гранник Платона); М2 — куб (равнорёбернный 6-гранник Платона); М3 — призма ортогональная натуральная (с целочисленным соотношением рёбер и объёмной диагональю 2/3/6/7); М4 — клин (призма 3-угольная); М5 — пирамида 3-угольная (4-гранник неравнорёберный); М6 — пирамида 3-угольная усечённая; М7 — пирамида 4-угольная (5-гранник неравнорёберный); М8 — пирамида 4-угольная усечённая; М9 — конус круговой; М10 -конус круговой усечённый.
B серии опытов с пластмассовыми композициями применялась следующая оснастка, изготовленная из термопластичных материалов: стойки, полые конусы (усечённые, с осевым отверстием), аналогичные полусферы. Из этих деталей (в сочетании с металлическими распорными втулками) составлялись соосные композиции, где изменялось взаимное расположение конусов или полусфер, в том числе раструбом вниз или вверх. Весовым испытаниям подверглись 34 композиции, содержащие от одного до четырёх конусов и от одной до четырёх полусфер.
Подводя итоги рассматриваемой работы выполненной на общественных началах в 1999 году, необходимо отметить, что данными опытами была охвачена лишь ничтожная часть из известных объемных геометрических тел и композиций. Существует множество эвристических параметров, реализация которых в подобных экспериментах могла бы, возможно, дать не менее яркие результаты, представляющие интерес для различных областей науки и техники.
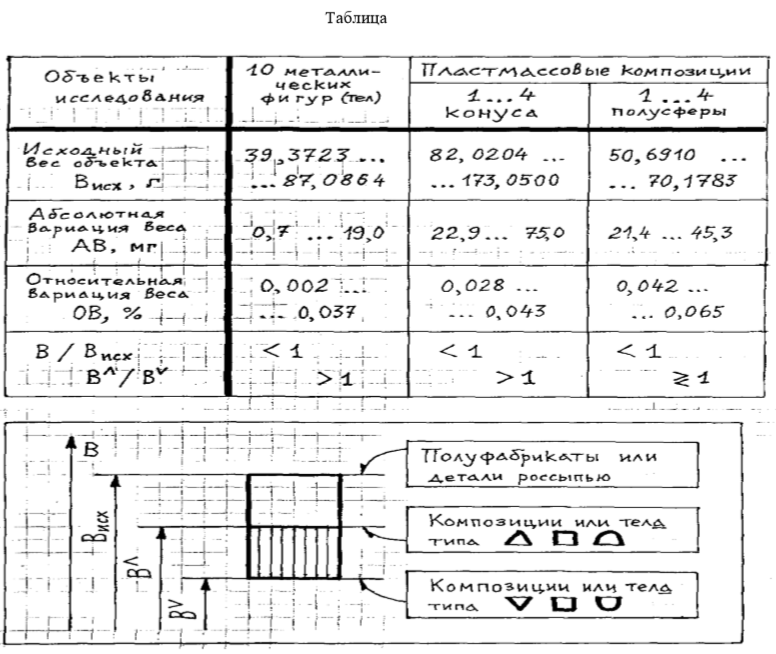
Обобщённые итоги экспериментов представлены в таблице 1 и на рис.1, где использованы следующие обозначения:
В — вес композиции (объекта в сборе), г ;
Висх — исходный вес объекта (плоского полуфабриката и нескольких проволочек — для металлических композиций; совокупности деталей, образующих пластмассовую композицию), г ;
В∧ и Вv — значения веса композиции соответственно при нижнем и верхнем положениях её открытого основания (раструба);
АВ — абсолютная вариация веса, равная разности предельных значений веса объекта, мг;
OB — относительная вариация веса (равная отношению абсолютной вариации к среднему весу объекта), %.
Абсолютная вариация веса объектов в ряде случаев достигала весьма существенных значений (до 75 мг), т.е. на уровне 3-ей и 2-ой цифр после запятой, в граммах. Следовательно, указанная вариация может в десятки раз превышать погрешность весов.
Изменение веса объекта (при постоянной массе!) объясняется по мнению авторов, наличием микроэнергетических процессов в «условно-оптической системе» объекта под влиянием теллурических и космических потоков энергии, по-разному трансформируемых в телах разной формы и разной ориентации. Объекты, возможно, ведут себя, как некие волноводы колебаний высокой частоты.
В пользу данного предположения говорит следующее важнейшее наблюдение» При взвешивании испытуемых объектов не происходило однозначной фиксации веса: стрелка, отсчитывающая десятые доли миллиграмма, продолжала медленно ползти вперёд. Очевидно, микроэнергетический процесс в объекте продолжал развиваться.
Композиции из нескольких соосных конусов или полусфер, как правило, были более активными, чем одиночные тела. Композиции из нескольких соосных полусфер, как правило, были более активными, чем композиции из конусов.
Во всех опытах вес объекта в объёмном (собранном) виде оказывался меньше, чем его исходный вес (т.е. вес плоской заготовки или суммарный вес его отдельных деталей россыпью).
Во всех опытах вес объекта при расположении его открытого основания (раструба) внизу оказывался больше, чем при этом основании вверху.
По результатам исследований можно сделать следующие обобщенные выводы:
- Вес объёмной композиции (полуоткрытого полого тела) не равен суммарному весу её деталей при неизменном количестве вещества.
- Вес композиции (тела) зависит от её геометрической формы и положения в пространстве.
- Исходный вес деталей объекта всегда был больше, чем вес собранного объекта.
- По гипотезе авторов можно предполагать, что вышеназванные свойства обусловлены вторичными микроэнергетическими потоками в объекте, создающими своеобразную «силу реакции» на объекте, либо — изменяющими величину гравитационного ускорения, входящего в формулу Ньютона для силы и массы.
- Полученные результаты необходимо принимать во внимание при проведении научно-исследовательских и опытно-конструкторских работ по тематике архитектурного, инженерного и экологического характера.
Сводные данные объектов исследования.
Автор: Плужников А. И., профессор, академик МАИ и МАЭИН, Ерошненко В.М., профессор, д.т.н.
![]()
