Одним из самых простых и одновременно самых сложных и странных объектов является лента Мёбиуса. Несмотря на всю неординарность данной фигуры её с легкостью можно сделать самостоятельно и провести все эксперименты, которые описываются в этой статье.
Лента Мёбиуса – простейшая неориентируемая поверхность, которая является односторонней в трёхмерном пространстве. Её часто называют ещё поверхностью Мёбиуса и относят к непрерывным (топологическим) объектам.
Согласно легенде, немецкий астроном, математик и механик Август Фердинанд Мёбиус открыл этот объект после того, как служанка, работающая в его доме, сшила тканевую ленту в кольцо, перевернув по невнимательности один из ее концов. Увидев результат, вместо того, чтобы отругать незадачливую девушку Мёбиус произнес: «Ай да, Марта! Девочка не так уж глупа. Ведь это же односторонняя кольцевая поверхность. У ленточки нет изнанки!»

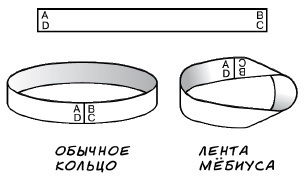
Сделать ленту Мёбиуса очень просто: возьмите ленту ABCD, а после сверните таким образом, чтобы точки A и D соединились с B и C.
Получается обычная на первый взгляд фигура, которая имеет очень интересные свойства.
Необычные свойства ленты Мёбиуса
Односторонность
Все мы привыкли к тому, что у поверхностей всех объектов, с которыми мы сталкиваемся в реальном мире (например, листок бумаги) две стороны. Но поверхность ленты Мёбиуса односторонняя. Это легко можно проверить путем закрашивания ленты. Если взять карандаш и начать окрашивать ленту с любого места, не переворачивая, то в конечном итоге, лента окажется полностью закрашена.
«Если кто-то попробует раскрасить только одну сторону поверхности ленты Мёбиуса, то пусть лучше сразу погрузит ее в ведро с краской», Р. Курант и Г. Роббинс, «Что такое математика?»
Поверхность ленты Мёбиуса непрерывная
Это легко проверяется следующим образом: если в любом месте на ленте поставить точку, то ее можно соединить с любой другой точкой на поверхности ленты, не пресекая края. Таким образом, получается, что поверхность этого объекта непрерывная.
У ленты Мёбиуса нет ориентированности
Если бы вы смогли пройти через всю ленту Мёбиуса, то в момент возвращения в начальную точку путешествия вы бы превратились в зеркальное отражение самого себя.
Если ленту разрезать вдоль посередине, то в таком случае получается всего одна лента, хотя логика говорит о том, что их должно быть две, а если разрезать, отступив от края на треть ширины ленты, то получится уже два кольца сцепленных вместе — маленькое и большое. Сделав затем продольный разрез малого кольца посередине, в итоге, получим два переплетенных кольца одинаковых в размере, но разных по ширине.
Практическое использование ленты Мёбиуса
Уже существует довольно много изобретений, основанных на свойствах этого необычного топологического объекта. Например, красящая лента в матричных принтерах, скрученная в ленту Мёбиуса, служит гораздо дольше, поскольку износ в этом случае происходит равномерно по всей ее поверхности. А скрученные в форме этого геометрического объекта лопасти кухонного миксера или бетоносмесителя снижают энергозатраты на 20%, и при этом качество полученной смеси улучшается.
Существует гипотеза, что полимер ДНК, представляющий собой двойную спираль, является фрагментом ленты Мёбиуса и по этой причине код ДНК так труден для расшифровки и понимания.
Некоторые физики, говорят о том, что оптические эффекты основаны на тех же свойствах, которыми обладает этот парадоксальный объект, так наше отражение в зеркале — это частный случай, одного из свойств ленты Мёбиуса.
Еще одна гипотеза, связанная этим математическим объектом — это то, что сама наша Вселенная, возможно, замкнута в такую ленту и у нее есть своя зеркальная копия. Поскольку, если все время двигаться в одном направлении по ленте Мёбиуса, то, в конце концов, окажемся в начальной точке нашего путешествия, но уже в своем зеркальном отображении.
Загадочная бутылка Клейна
На основе ленты Мёбиуса существует ещё одна удивительная фигура – бутылка Клейна. Она представляет с собой бутылку, у которой на дне есть отверстие. Горлышко бутылки удлинено и загнуто, проходя в одну из стенок самой бутылке.
Такую фигуру невозможно воспроизвести в обычном трехмерном пространстве, ведь горлышко не должно касаться стенки бутылки и соединено с отверстием в ее дне. Таким образом, получается поверхность, которая имеет всего одну сторону. Бутылка Клейна и лента Мёбиуса до сих пор привлекает внимание учёных, а также писателей.
А. Дейч в одном из своих рассказов писал о том, как однажды в Нью-Йоркском метро пути пересеклись и весь метрополитен стал напоминать ленту Мёбиуса, а электрички, идущие по путям, стали пропадать, вновь появляясь, только спустя несколько месяцев.
В книге Александра Митча «Игра в поддавки» герои попадают в пространство, которое напоминает бутылку Клейна.
Мир до сих пор остаётся для нас огромной загадкой, и кто знает, какие ещё причуды пространства откроют учёные в ближайшем будущем.
![]()